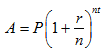Reconociendo lo Aprendido Unidad 3

En esta unidad se vieron los temas mayormente relacionados con la derivación de los limites, también en la aplicación de la derivada en problemas matematicos, unos temas algo extensos pero realmente faciles de comprender y aplicar.

 

La Derivada a Partir del Concepto de Limite 

La derivada es uno de los conceptos más importante en matemáticas. La derivada es el resultado de un límite y representa la pendiente de la recta tangente a la gráfica de la función en un punto.

 

 

Video

 

 https://youtu.be/UKTfer8PHv4

 

    Ejercicios

 

en , y

en

en

Tecnicas de Derivacion

Generalmente la derivación se lleva acabo aplicando fórmulas obtenidas mediante la regla general de la derivación y que calcularemos a continuación, de estas podemos derivar las funciones algebraicas, trascendentales, sucesivas y combinadas. 

 

Video

https://youtu.be/D-1VYdAQnNY 

 

 Trazado de Graficas con Derivadas

El trazado de la gráfica de una función derivable es un tipo de representación gráfica que permite conocer intuitivamente el comportamiento de dicha función.

Video 

 https://youtu.be/Q73XxigqTP8

 

Variables de Cambio Relacionadas y Optimizacion 

 

Optimización

Video

https://youtu.be/PLyfy99_4ug 

https://youtu.be/_exKGOyFZ50 

 

Regla de L'hopital 

La regla de L'Hôpital nos ayuda a evaluar límites de las formas indeterminadas $\dfrac{0}{0}$start fraction, 0, divided by, 0, end fraction y $\dfrac{\infty}{\infty}$start fraction, infinity, divided by, infinity, end fraction.

En otras palabras, nos ayuda a encontrar $\displaystyle\lim_{x\to c}\dfrac{u(x)}{v(x)}$limit, start subscript, x, \to, c, end subscript, start fraction, u, left parenthesis, x, right parenthesis, divided by, v, left parenthesis, x, right parenthesis, end fraction, donde $\displaystyle\lim_{x\to c}u(x)=\lim_{x\to c}v(x)=0$limit, start subscript, x, \to, c, end subscript, u, left parenthesis, x, right parenthesis, equals, limit, start subscript, x, \to, c, end subscript, v, left parenthesis, x, right parenthesis, equals, 0 (o, alternativamente, donde ambos límites son iguales a $\pm\infty$plus minus, infinity).

La regla esencialmente dice que si el límite $\displaystyle\lim_{x\to c}\dfrac{u'(x)}{v'(x)}$limit, start subscript, x, \to, c, end subscript, start fraction, u, prime, left parenthesis, x, right parenthesis, divided by, v, prime, left parenthesis, x, right parenthesis, end fraction existe, entonces los dos límites son iguales:

$\displaystyle\lim_{x\to c}\dfrac{u(x)}{v(x)}=\displaystyle\lim_{x\to c}\dfrac{u'(x)}{v'(x)}$

 

$Video$

 https://youtu.be/CqsNjPWC8XA​

 

 

Conclusión 

En conclusión todos estos estan relacionados para aplicar uno se debe de tener como base el anterior y asi sucesivamente.

Fueron temas relativamente faciles aunque tenian su grado de dificultan y a veces me confundia un poco.

 

Bibliografia

http://descartes.cnice.mec.es/materiales_didacticos/Derivada_de_una_funcion/Derivada_de_una_funcion.htm

https://www.superprof.es/apuntes/escolar/matematicas/calculo/derivadas/ejercicios-de-la-definicion-de-derivada.html 

 

https://www.mat.uson.mx/~jldiaz/Documents/Derivadas/Tecnicas-Derivacion-cb.pdf 

https://sites.google.com/site/puente200222/trazado-de-graficas-de-funciones-derivables

https://www.mat.uson.mx/~jldiaz/Documents/Derivadas/FTRazon.pdf 

https://www.feandalucia.ccoo.es/docu/p5sd6071.pdf 

 https://es.khanacademy.org/math/differential-calculus/dc-context-app/dc-lhopital-composite-exp/a/lhopitals-rule-review

Limites

Durante esta unidad estudiamos los limites, sus leyes, como identificarlos, como graficarlos, así que acontinuación mostrere un poco de lo aprendido.

Introducción a los Limites

Uno de los análisis bases para una función es estudiar su continuidad y los valores en el que posiblemente ésta no exista. Por lo tanto, estudiar a la función en entornos reducidos de estos valores y observando el comportamiento de ella misma, es lo que llamamos límites de una función.

La simbología que usaremos para estudiar los límites de una función acercándose a algún valor en específico es la siguiente:

 Donde, lim es la manera abreviada de escribir límite, x → a se lee “cuando x tiende al valor a en la función”, es decir, cuando la variable x toma valores muy cercanos al valor a.

Video 

https://youtu.be/o2UTk8bsLS0 

Ejercicios

Continuidad

Intuitivamente, una función es continua si su gráfica puede dibujarse de un solo trazo, es decir, sin levantar el lápiz del papel.

Video

https://youtu.be/sHuqCyEVNCs 

Ejercicios

 

Leyes de los Limites

Video

 https://youtu.be/PZhTK99o1pk

Ejercicios

 

 Limites al Infinito

Un límite al infinito es aquel al que tiende f(x) cuando la variable x se hace tan grande, tanto en positivo como en negativo, como queramos. Entonces la función f(x) puede tender a un valor finito o puede diverger a infinito (límite infinito).

Limite infinito 

Se dice que existe límite infinito cuando la función f(x) llega a valores que crecen continuamente, es decir que se puede hacer la función tan grande como queramos. Se dice que f(x) diverge a infinito. Para ello, el valor al que tienda la variable independiente x puede ser tanto a un número finito, como tender al infinito (límites al infinito). 

Video

https://youtu.be/YwOBnHe1sz8 

Ejercicios

Formas Indeterminadas

 Video

https://youtu.be/r6VWu2sxE7c 

Ejercicios

 Límites de las Funciones Trigonométricas

 

Video

https://youtu.be/PgOU6hYfk4s

    Ejercicios

 Resumen

Cuando el profesor comenzo a explicar el tema la verdad yo no tenia muy buena idea de que se trataba, lo confundia con las asíntotas, pero despues de la explicación del profesor al desarrollar ejercicios durante las clases fui comprendiendo mejor que eran los limites, cuando un limite es indeterminado, y no se que tanta aplicación le pueda dar para mi diario vivir pero son conocimientos generales que en algun momento necesitare asi sea para ayudarle a mi hijo hacer las tareas.

 

Bibliografias:

https://miprofe.com/limites-introduccion/ 

https://matemovil.com/wp-content/uploads/2018/07/L%C3%ADmites-Ejercicios-Propuestos-PDF.pdf

https://matemovil.com/leyes-y-propiedades-de-los-limites-ejercicios-resueltos/ 

https://www.universoformulas.com/matematicas/analisis/limites-al-infinito/#google_vignette 

https://www.universoformulas.com/matematicas/analisis/limites-infinitos/

https://es.slideshare.net/ftorrealba/ejercicios-resueltos-de-formas-indeterminadas 

https://canvas.utp.edu.pe/courses/10738/files/541479

https://www.matesfacil.com/resueltos-continuidad.htm 

https://www.superprof.es/apuntes/escolar/matematicas/calculo/funciones/ejercicios-y-problemas-resueltos-de-continuidad.html

 

Reconociendo lo Aprendido de Funciones

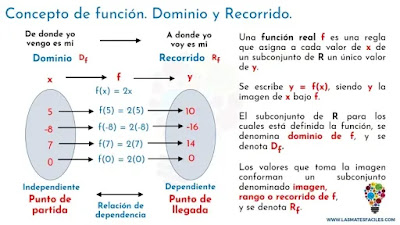
Funciones reales, dominio y rango 

 Video

 https://youtu.be/H40lcwlgPMk

Ejercicios

 

 Evaluación de una función

 

 

 

 Video 

 https://youtu.be/tvUoOZDRAks

 

Ejercicios

 

Gráfica de una función

Video

https://youtu.be/PY3hri_MWfg

Ejemplos

 

 

 

 

 

Funciones Crecientes y Decrecientes

 

Video

https://youtu.be/NHtXOV7XLQc 

Ejemplos

 

Desplazamiento vertical de una gráfica

 

Video

https://youtu.be/-lqLdZd87Ck

 

Ejemplos

 

Desplazamiento horizontal de una gráfica

 

Video

https://youtu.be/gZKtdHnT14M

 

Ejemplo
 

 

La inversa de una función

Video

https://youtu.be/TxRpKrQJsdw 

Ejemplos

Clases de funciones: lineales, potencia, raíz, recíprocas, valor absoluto

 

Video

https://youtu.be/nQNfi9Tew2g 

 

Intercepto con los ejes coordenados

 Video

 https://youtu.be/zRl2AL99OA0

 

Ejemplo

Ecuaciones de la línea recta

 

Video

https://youtu.be/ciIutiTfcbc 

Ejemplo

 Aplicaciones de las ecuaciones de la línea recta

https://youtu.be/dr5LoGyDHLM 

 

Aplicaciones de las funcione

Aplicación técnica y práctica de las funciones

 

Todo lo que hemos visto de las funciones tiene una gran importancia en la Tecnología. En muchos casos las funciones que modelan un proceso tecnológico son conocidas y basta con aplicarlas para obtener, por ejemplo, el valor de una determinada variable en el proceso. En otros casos es necesario, partiendo del conocimiento general de las características físicas de un sistema, determinar el modelo matemático que lo rige o sea hallar la función que nos permita hallar variables de interés para el control o seguimiento del proceso o sistema en cuestión.

 

Construcción de modelos matemáticos utilizando las funciones.

Con los datos experimentales, por ejemplo en forma de tabla, es posible hallar el modelo matemático que mejor ajusta a estos valores. Esto se hace utilizando herramientas matemáticas que hacen el ajuste de curvas o la regresión a partir de los datos de las variables dependientes e independientes. El tratamiento de estos temas excede el objetivo de este curso y por tanto le recomendamos al interesado consultar bibliografía al respecto.

Ejercicios:

La presión en una marmita se describe por la ecuación:

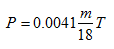
donde P es la presión en atmósferas, m es la masa de agua en g y T la temperatura en °K.

Obtenga la gráfica de P vs T para m=9, 18 y 36 g en el rango de 0 a 200 °C. Si la presión no debe exceder 3.5 atm, ¿Se alcanzará este valor en alguno de los casos?.

 

Una reacción química transcurre según la ley:

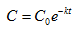
donde k es la constante específica de velocidad y t es el tiempo en horas. Grafique esta función para Co= 2, k=0.75 y 0 <= t <=2

Si se tienen los valores de concentración y tiempo que se indican en la tabla siguiente, determine el valor de k transformando la ecuación mediante la aplicación de logaritmo neperiano a ambos lados.

 

 

Aplicaciones de las funciones exponenciales y logarítmicas.

Las funciones exponenciales se aplican en aquellos casos en los que la rapidez de cambio de una magnitud es proporcional a su valor en el momento. Este concepto lo veremos con más claridad cuando estudiemos las derivadas y las integrales.

Entre las aplicaciones se encuentran:

§                     El cálculo de interés

§                     La descomposición de sustancias radioactivas y otras reacciones químicas de primer orden

§                     El crecimiento de población

§                     La tasa de depreciación de equipamiento

En el cálculo del interés se utiliza la siguiente fórmula:

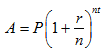
donde
A es el dinero acumulado.

P es la cantidad inicial de dinero.

r es la tasa de interés anual compuesta n veces por año

t es el número de años.

Ejemplo se invierten $1,000 a una tasa de 12.5% anual compuesta anualmente por 10 años. Utilizando la formula anterior calcule la cantidad acumulada después de los 10 años:

P = $1000

r = 12.5% = .125

n = 1

t = 10

A = $1000(1 + .125)¹⁰

A = $1000(1.125)¹⁰

A = $1000(3.247)

A = $3,247

 

En el crecimiento bacteriano la fórmula comúnmente utilizada es:

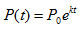
donde P(t) es la población en el instante t, P₀ es la población inicial (cuando t = 0), y k es la constante de crecimiento, que depende de las características del cultivo.

Ejemplo: Un cultivo bacteriano tiene una constante de velocidad de crecimiento  k = .03 y un conteo inicial arrojó el valor de 10000.

Después de 3 horas, la población del cultivo se calcula

P(t) = P₀e^kt

P₀ = 10000

k = .03

t = 3

P(t) = 10000 e^0.03(3)

P(t) = 10,940

 

 

 

 

 

Bibliografiia

 

http://www3.uacj.mx/CGTI/CDTE/JPM/Documents/IIT/sterraza/mate2016/funcion/func_ejem.html

https://www.cimat.mx/~cesar/calculo_verano_2011/tareas/soluciones05.pdf 

https://www.ck12.org/book/ck-12-conceptos-de-c%c3%a1lculo-en-espa%c3%b1ol/section/1.5/

https://algebraenpdf.blogspot.com/2018/12/desplazamiento-grafica-funciones.html 

https://www.problemasyecuaciones.com/funciones/inversa/funcion-inyectiva-suprayectiva-sobreyectiva-inversa-ejemplos-problemas-resueltos-calcular.html

http://pspc1.weebly.com/intercepto-en-los-ejes.html 

https://www.geogebra.org/m/PkPgbwTQ

https://navarrof.orgfree.com/Docencia/MatematicasII/M2UT1/ut1t4.htm